Author: Site Owner

Website Owner

Why I’m Here: Appreciating Forests in a New Way

January 23rd, 2018|0 Comments

.fusion-fullwidth-1 {
padding-left: px !important;
padding-right: px !important;
}

By Megan Wright, American Forests

I never really appreciated the Adirondack Mountains until I left them for Washington, D.C. As a budding college student eager to see what the world had to offer, the change to big-city life was what I wanted. When I left for school, I expected to miss my family, my dog. I did not expect to miss the view of the mountains on the horizon; the clean, crisp air; and the clear night skies that allowed me to see the Big Dipper from my front yard.

As a child growing up in New York (upstate, not the city), I got used to seeing forests all around me, which led me to assume that that kind of natural scenery was everywhere. I loved to take hikes with my friends and family every weekend, or walk my dog at the conservation area five minutes from my house. I took for granted the sense of serenity that forests brought me, making me feel as though I was, and am, a part of something bigger than myself.

Realizing just how important forests are to me is one of the many things that drew me to American Forests. I love D.C. and I love trees, and American Forests allowed me to combine the two with important initiatives like their Community ReLeaf program.

This program focuses on urban forests across the country, working to plant more trees in cities, assess damage on tree canopies, and encourage people of all ages to learn the importance of forests. For D.C. in particular, American Forests engages with disenfranchised communities and works to create greenspace across the city. For example, they were able to turn a three-acre vacant lot into a public greenspace that includes a children’s discovery area, performance stages, a fitness track, art installations, and an urban research farm.

The work that American Forests is doing in urban areas is essential. According to the U.S. Forest Service, more than 80 percent of Americans live in urban areas. That number will surely grow as we become a more urbanized nation and, in doing so, we have to shift the way that we incorporate forests into our daily lives.

Urban forests play a key role in promoting the health and happiness of communities. They filter air, control stormwater runoff, conserve energy, and provide animal habitats. Forests improve the well-being of people living in cities as well, as they reduce stress, create places to relax and play, spur neighborly interaction and decrease noise pollution.

To me, working with American Forests allows me to get back some of what I miss from home, and to share it with others. Even in a city as big and bustling as Washington, D.C., people can still connect with forests and nature thanks to programs like Community ReLeaf. Although it’s not the same as being a 20-minute drive from the Adirondacks or being able to take a hike whenever I please, American Forests is helping me connect with forests in a new way.

As a policy intern, I will be able to help make sure that all communities have access to greenspace and trees; that people in urban areas will be able to experience a little of what I had growing up, right outside their front doors.

By working with an organization that is so committed to restoring, protecting and integrating forests, I am able to have the chance to care for a part of nature that has cared for me the majority of my life. After all, we are a part of nature, not separate from it, so by caring for forests, we are essentially caring for ourselves.

The post Why I’m Here: Appreciating Forests in a New Way appeared first on American Forests.

Forest Digest: January 21, 2018

January 21st, 2018|Tags: , , , , |0 Comments

.fusion-fullwidth-1 {
padding-left: px !important;
padding-right: px !important;
}

Check out what’s happened this week in forestry news!

Credit: Francois Kehas-Dewaghe/Los Padres ForestWatch

Peru’s Newest National Park Safeguards 2 Million Acres of Amazon Rainforest – EcoWatch

The recently approved Yaguas National Park will be located in the northern region of Loreto in Peru. The expanse of rainforest it encompasses — about the same size as Yellowstone National Park — is home to a diverse wildlife population. In addition to conserving the region’s biodiversity, the Peruvian government intends to protect the sacred lands of the indigenous communities in the area.

Los Angeles needs open space for wildlife and for our sanity – Los Angeles Times

An issue that arises with the expansion of residential developments in Los Angeles is the threat of losing open, undeveloped land. The combined efforts of Citizens for Los Angeles Wildlife and Laurel Canyon Association were able to preserve open space by raising money to buy a mountain ridge in Hollywood Hills. In the Santa Ana and Santa Monica mountain areas, the California Department of Fish and Wildlife’s process for issuing “depredation permits” to residents has been changed to give mountain lions a three-strike policy.

Sustainably harvesting roundwood for use in bioenergy is good for forests – Politico

In this interview, longtime forester Randy Rogillio discusses the importance of responsible forest management techniques. By sustainably harvesting forests, the overall health of the forests can be maintained while also using the harvested wood to serve numerous products, such as lumber, paper, and fuel pellets. He explains the process of “thinning,” and how the by-products of this process are turned into wood pellets for the biomass industry. He also explains the aftercare of harvested forests.

Researchers find post-fire logging harms spotted owls – Phys.org

According to a recent study, the reason that California’s rare spotted owls are abandoning breeding territories after intense wildfires is due to post-fire logging, not the actual fires. In the aftermath of wildfires, the remains of the forest attract small mammals, which the owls then hunt. While the spotted owls have evolved to survive off the remnants of wildfires, the growing practice of post-fire logging threatens their livelihood.

Europe’s lost forests: Coverage has halved over 6,000 years – Science Daily

In a study published in Nature’s Scientific Reports, scientists analyzed pollen samples from various locations and determined that most of Europe was once covered by trees. The study aims to establish how Europe’s forests have changed over the past 11,000 years. Researchers hope the data collected for this study can be used to understand how future forestry techniques may influence wildlife habitat changes.

The post Forest Digest: January 21, 2018 appeared first on American Forests.

The claim of reduced uncertainty for equilibrium climate sensitivity is premature

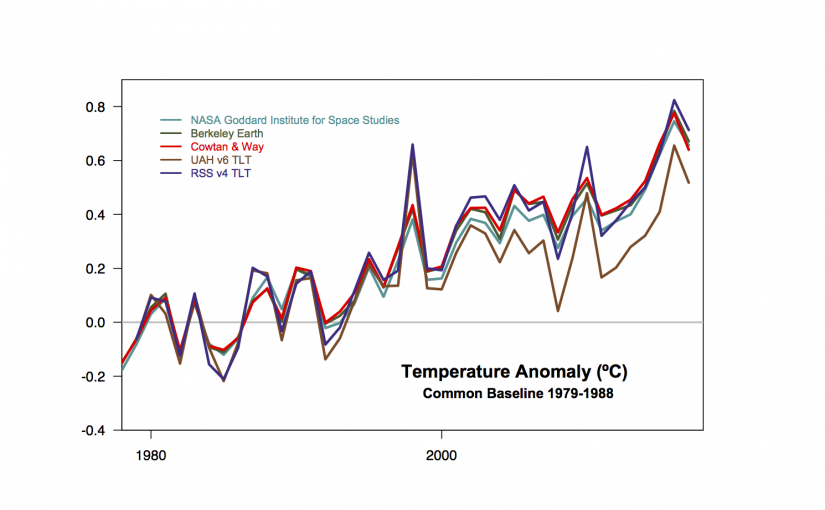
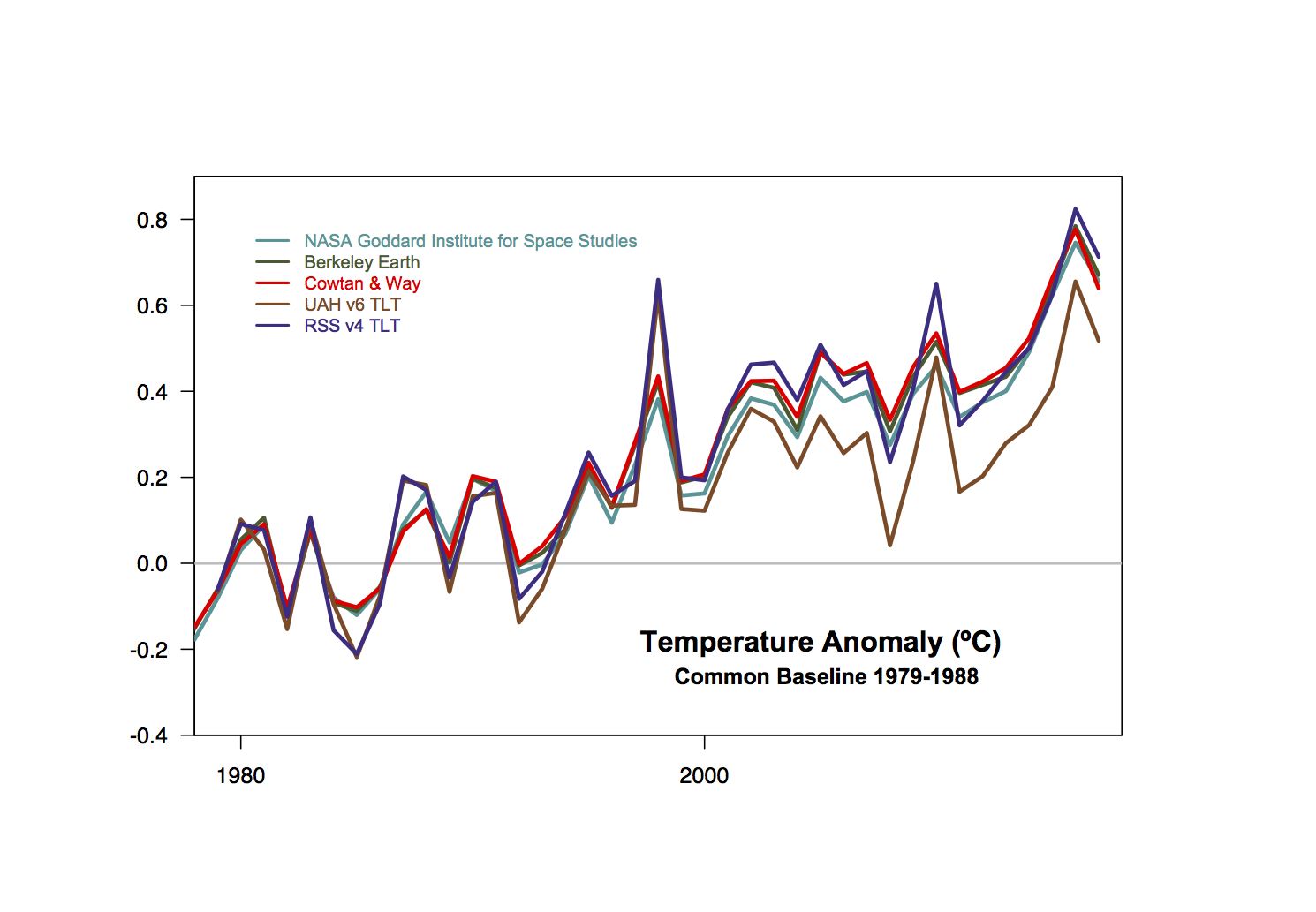
A recent story in the Guardian claims that new calculations reduce the uncertainty associated with a global warming:

A revised calculation of how greenhouse gases drive up the planet’s temperature reduces the range of possible end-of-century outcomes by more than half, …

It was based on a study recently published in Nature (Cox et al. 2018), however, I think its conclusions are premature.

The calculations in question involved both an over-simplification and a set of assumptions which limit their precision, if applied to Earth’s real climate system.

They provide a nice idealised and theoretical description, but they should not be interpreted as an accurate reflection of the real world.

There are nevertheless some interesting concepts presented in the analysis, such as the connection between climate sensitivity and the magnitude of natural variations.

Both are related to feedback mechanisms which can amplify or dampen initial changes, such as the connection between temperature and the albedo associated with sea-ice and snow. Temperature changes are also expected to affect atmospheric vapour concentrations, which in turn affect the temperature through an increased greenhouse effect.

However, the magnitude of natural variations is usually associated with the transient climate sensitivity, and it is not entirely clear from the calculations presented in Cox et al. (2018) how the natural variability can provide a good estimate of the equilibrium climate sensitivity, other than using the “Hasselmann model” as a framework:

(1)   \begin{equation*} C \frac{d \Delta T}{dt} = Q - \lambda \Delta T = N. \end{equation*}

Cox et al. assumed that the same feedback mechanisms are involved in both natural variations and a climate change due to increased CO2. This means that we should expect a high climate sensitivity if there are pronounced natural variations.

But it is not that simple, as different feedback mechanisms are associated with different time scales. Some are expected to react rapidly, but others associated with the oceans and the carbon cycle may be more sluggish. There could also be tipping points, which would imply a high climate sensitivity.

The Hasselmann model is of course a gross simplification of the real climate system, and such a crude analytical framework implies low precision for when the results are transferred to the real world.

To demonstrate such lack of precision, we can make a “quick and dirty” evaluation of how well the Hasselmann model fits real data based on forcing from e.g. Crowley (2000) through an ordinary linear regression model.

The regression model can be rewritten as y = \beta_1 x_1 + \beta_2 x_2 + \eta, where y = Q, x_1 = \frac{d \Delta T}{dt}, and x_2 = \Delta T. In addition, \beta_1 = C and \beta_2 = \lambda are the regression coefficients to be estimated, and \eta is a constant noise term (more details in the R-script used to do this demonstration).

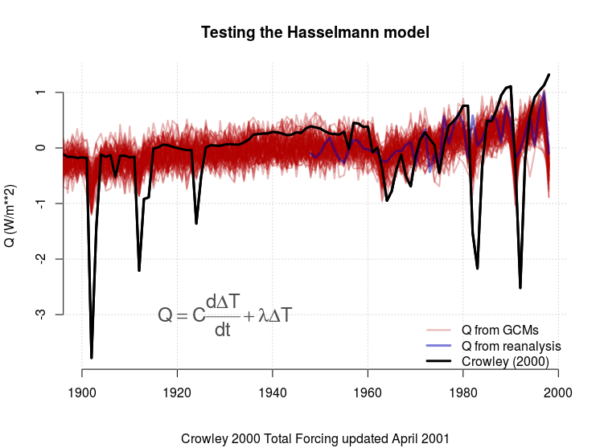
Figure 1. Test of the Hasselmann model through a regression analysis, where the coloured curves are the best-fit modelled values for Q based on the Hasselmann model and global mean temperatures (PDF).

It is clear that the model fails for the dips in the forcing connected volcanic eruptions (Figure 1). We also see a substantial scatter in both C (some values are even negative and hence unphysical) and \lambda (Figure 2).

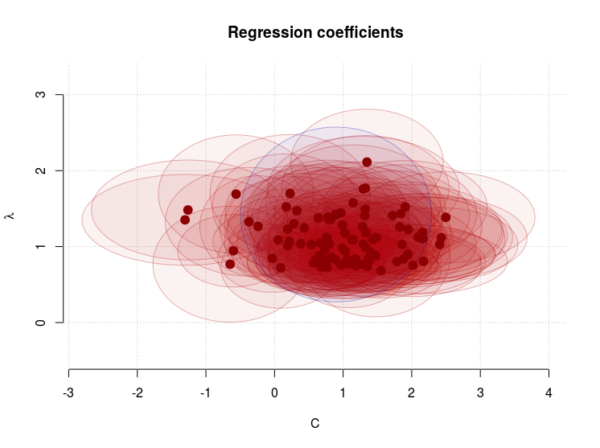
Figure 2. The regression coefficients. Negative values for C are unphysical and suggest that the Hasselmann model is far from perfect. The estimated error margins for C are substantial, however, and also include positive values. Blue point shows the estimates for NCEP/NCAR reanalysis. The shaded areas cover the best estimates plus/minus two standard errors (PDF).

The climate sensitivity is closest associated with \lambda, for which the mean estimate was 1.11W/(m^2 K), with a 5-95-percentile interval of 0.74-1.62W/(m^2 K).

We can use these estimates in a naive attempt to calculate the temperature response for a stable climate with d \Delta T/dt=0 and a doubled forcing associated with increased CO2.

It’s plain mathematics. I took a doubling of 1998 CO2-forcing of 2.43W/m^2 from Crowley (2000), and used the non-zero terms in the Hasselmann model, \Delta T_{2 \times CO2} = Q_{2 \times CO2}/\lambda.

The mean temperature response to a doubled CO2-forcing for GCMs was 2.36K/Q_{2 CO2}, with a 90% confidence interval: 1.5 – 3.3K/Q_{2 \times CO2}. The estimate from reanalysis was 1.71K/Q_{2 \times CO2}

The true equilibrium climate sensitivity for the climate models used in this demonstration is in the range 2.1 – 4.4 K/Q_{2 \times CO2}, and the transient climate sensitivity is 1.2 – 2.6K/Q_{2 \times CO2} (IPCC AR5, Table 8.2).

This demonstration suggests that the Hasselmann model underestimates the climate sensitivity and the over-simplified framework on which it is based precludes high precision.

Another assumption made in the calculations was that the climate forcing Q looks like a white noise after the removal of the long-term trends.

This too is questionable, as there are reasons to think the ocean uptake of heat varies at different time scales and may be influenced by ENSO, the Pacific Decadal Oscillation (PDO), and the Atlantic Multi-decadal Oscillation (AMO). The solar irradiance also has an 11-year cycle component and volcanic eruptions introduce spikes in the forcing (see Figure 1).

Cox et al.’s calculations were also based on another assumption somewhat related to different time scales for different feedback mechanisms: a constant “heat capacity” represented by C in the equation above.

The real-world “heat capacity” is probably not constant, but I would expect it to change with temperature.

Since it reflects the capacity of the climate system to absorb heat, it may be influenced by the planetary albedo (sea-ice and snow) and ice-caps, which respond to temperature changes.

It’s more likely that C is a non-linear function of temperature, and in this case, the equation describing the Hasselmann model would look like:

(2)   \begin{equation*} C(T) \frac{d \Delta T}{dt} = Q - \lambda \Delta T = N \end{equation*}

Cox et al.’s calculations of the equilibrium climate sensitivity used a key metric \psi which was derived from the Hasselmann model and assumed a constant C: \psi = \sigma_T/ \sqrt{-\ln(\alpha_{1T})}. This key metric would be different if the heat capacity varied with temperature, which subsequently would affect the end-results.

I also have an issue with the confidence interval presented for the calculations, which was based on one standard deviation 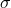\sigma. The interval of x \pm \sigma represents a 66% probability, and can be illustrated with three numbers: and two of them are “correct” and one “wrong”, which means there is a 1/3 chance that I pick the “wrong” number if I were to randomly pick one of the three.

To be fair, the study also stated the 90% confidence interval, but it was not emphasised in the abstract nor in the press-coverage.

One thing that was not clear, was whether the analysis, that involved both observed temperatures from the HadCRUT4 dataset and global climate models, took into account the fact that the observations do not cover 100% of Earth’s surface (see RC post ‘Mind the Gap!’).

A spatial mask would be appropriate to ensure that the climate model simulations provide data for only those regions where observations exists. Moreover, it would have to change over time because the thermometer observations have covered a larger fraction of Earth’s area with time (see Figure 3).

An increase in data coverage will affect the estimated variance \sigma_T and one-year autocorrelation \alpha_{1T} associated with the global mean temperature, which also should influence the the metric \psi.

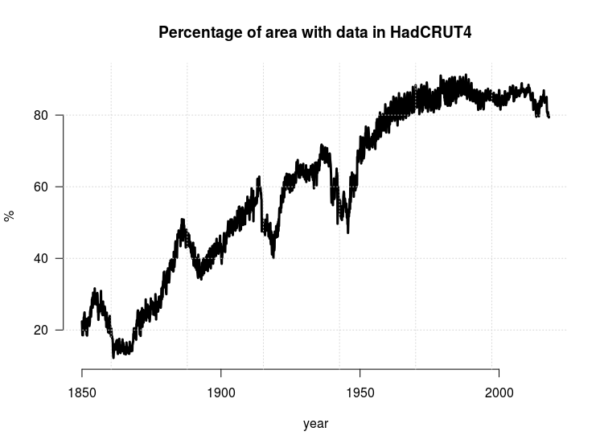
Figure 3. The area of Earth’s surface with valid temperature data (PDF).

My last issue with the calculations is that the traditional definition of climate sensitivity only takes into account changes in the temperature. However, there is also a possibility that a climate change involves a change in the hydrological cycle. I have explained this possibility in a review of the greenhouse effect (Benestad, 2017), and this possibility would add another term the equation describing the Hasselmann model.

I nevertheless think the study is interesting and it is impressive that the results are so similar to previously published results. However, I do not think the results are associated with the stated precision because of the assumptions and the simplifications involved. Hence, I disagree with the following statement presented in the Guardian:

These scientists have produced a more accurate estimate of how the planet will respond to increasing CO2 levels

References


  1. P.M. Cox, C. Huntingford, and M.S. Williamson, “Emergent constraint on equilibrium climate sensitivity from global temperature variability”, Nature, vol. 553, pp. 319-322, 2018. http://dx.doi.org/10.1038/nature25450


  2. T.J. Crowley, “Causes of Climate Change Over the Past 1000 Years”, Science, vol. 289, pp. 270-277, 2000. http://dx.doi.org/10.1126/science.289.5477.270


  3. R.E. Benestad, “A mental picture of the greenhouse effect”, Theoretical and Applied Climatology, vol. 128, pp. 679-688, 2016. http://dx.doi.org/10.1007/s00704-016-1732-y

2017 temperature summary

This is a thread to discuss the surface temperature records that were all released yesterday (Jan 18). There is far too much data-vizualization on this to link to, but feel free to do so in the comments. Bottom line? It’s still getting warmer.

Why I’m Here: Telling the Forest’s Story

January 17th, 2018|0 Comments

.fusion-fullwidth-1 {
padding-left: px !important;
padding-right: px !important;
}

By Leah Rambadt, American Forests

For most of my life, I’ve lived in the Blue Ridge Valley. Though I’ve been on numerous road trips with my family to almost every state in the country, the Blue Ridge Mountains are important to me because they mean “home.”

When I head home for school breaks or the holidays, the first curve in the highway indicates I’m getting closer and closer to my hometown. When I leave, the absence of curves and inclines mark the distance I’ve traveled away.

I grew up believing the mountains would never change. The trees covering them may go through the cycle of green leaves in the summer, an explosion of color in the fall, bare in the winter, and sprouting buds in the spring, but the mountains themselves wouldn’t change.

Now, it seems like there’s something different every time I go home. Sometimes the trees look like their leaves have changed colors or fallen off faster, or look like they’re growing back slower. Sometimes a mountain I remember being covered in trees looks more sparse, or has a new house or building on it. And sometimes, a part of the highway is under construction to expand the width of the roadway.

When I see these changes, I wish a tree or an entire forest would sprout up and grow until those changes disappear, and everything looks the way it used to. I know that isn’t possible, so instead, I’d like to learn more about American Forests’ urban forestry and reforestation projects to see if and how those techniques could be applied in my hometown.

Everything that lives has a story to tell. While the story I told above is how a part of the environment has had an impact on my life, I think the stories of the environment itself are the most overlooked and unheard. During my time at American Forests, my goal is to tell those stories — the environment’s stories — in a way that, hopefully, lets them be heard.

The post Why I’m Here: Telling the Forest’s Story appeared first on American Forests.

Forest Digest: January 14, 2018

January 14th, 2018|Tags: , , |0 Comments

.fusion-fullwidth-1 {
padding-left: px !important;
padding-right: px !important;
}

Gulf Hagas, Maine Credit: Lee Coursey

Find out what’s happened this past week in the world of forestry!

Forest Society of Maine announces completion of milestone conservation project near Gulf Hagas and Whitecap Mountain – The Piscataquis Observer

After four years of collaboration with the land owner, this project secured conservation of thousands of acres, including views from The Appalachian Trail, recreation sites, and habitats of the Eastern brook trout and Atlantic salmon.

After 1,000 Years, Iceland Is Growing Forests Again – Science Trends

After millions of years of changing climates, volcanic activity and the introduction of human settlement, Iceland’s forests dramatically decreased in size. However, things are starting to look up.

P.S. – Read about our contribution to reforesting Iceland through our project with Alcoa Foundation!

How forests could limit earthquake damage to buildings – physicsworld.com

Physicists in France have shown that certain seismic waves, known as Love waves, could be diverted away from the Earth’s surface as they pass through a forest containing trees of a certain height.

Swing Big for Climate-Safe Conservation – Huffington Post

Our VP of Conservation Programs, Jad Daley, examines how we can continue advancing conservation progress in an ever-changing climate.

Cataloguing primeval forests – DW

New technology is simplifying the process for taking inventory of biodiversity in ancient woodlands.

These Birds of Prey Are Deliberately Setting Forests on Fire – Science Alert

For over 40,000 years, Australian ‘firehawk raptors’ have reportedly assisted the spread of wildfire by carrying burning sticks in their beaks. While scientists are still working to figure out exactly why the birds are doing this, researchers do believe it’s done with intention.

The post Forest Digest: January 14, 2018 appeared first on American Forests.

Why I Am Here: Protecting My Sanctuary by Preserving Forests

January 10th, 2018|0 Comments

.fusion-fullwidth-1 {
padding-left: px !important;
padding-right: px !important;
}

By Emily Stringfellow, American Forests

After discovering how forests provide an escape from the daily pressures that life brings, they have become a sanctuary for me. Birds chirping, squirrels scrambling and deer tiptoeing all captivate my attention. Walking through a forest calms my mind and leaves me feeling refreshed. I have found that exploring forests has provided me with more peace of mind and stress relief than any other kind of exercise.

My hobby of walking through forests for mental benefits actually has a specific name: forest bathing. The term can be a little misleading when interpreted directly, as it does not involve taking a bath in the woods, but rather immersing yourself in a forest. Evidence from a study done by the Japanese government in the 1980s shows how forest bathing has many health benefits. Spending time in a forest reduces stress levels, lowers blood pressure, reduces risk of disease and stimulates creativity. Another study conducted in Japan found that forest bathing reduces depression. The health benefits from forest bathing are easy to obtain, as all it takes is a walk among the trees around you.

Because of how forests have positively impacted my mental health and can improve others’ mental health, American Forests quickly gained my interest. For these health benefits to remain easily obtainable, forests need to be preserved.

When I was younger, my family was fortunate enough to have a forest run along the side of our yard. I was always steps away from a completely different world full of a variety of plants and wildlife. The forest behind my house was a place to explore, imagine and escape after a day of sitting in a classroom. The neighborhood kids and I enjoyed playing in streams and hiding among the trees. I was heartbroken when we were informed that a neighborhood was being developed directly behind my family’s home and that our beloved forest would be lost to us. For years, I was accustomed to the excitement of seeing deer roaming close to our yard and the ability to escape from reality for a few hours. The trees slowly came down and houses were erected in their place. I had lost my sanctuary. This loss highlighted just how quickly a forest can disappear and gave me a greater appreciation for the next forest I found to escape to.

A few years later, I found a new sanctuary: Umstead State Park. Even though I am older and walk instead of play in these woods, they still have the same effect on my mental state. It is a place for me to relax and enjoy nature. My dog, Lily, usually joins me. She is the perfect hiking companion since she does not complain about the length of the hike or the weather, like my sisters do. As soon as I grab her leash, she runs around our kitchen in excitement. After a short drive, we turn onto a small road and are immediately surrounded by a forest. While hiking in this place, you would never know that there are multiple shopping centers less than a mile away. When it is time to leave, my dog always resists getting in the car. She wants to continue our journey through the forest.

Based on the peace of mind they afford and the joy they bring to me and my dog, I have come to the conclusion that protecting forests is a worthwhile cause of which I would like to be a part. Losing Umstead State Park would cause me to lose a place where I can receive the multitude of benefits that forests provide. American Forests presents the perfect avenue to advocate for forests and prevent my sanctuary — and those like it around the country — from being taken away again.

The post Why I Am Here: Protecting My Sanctuary by Preserving Forests appeared first on American Forests.

Forest Digest: January 7, 2018

January 7th, 2018|Tags: , , , , |0 Comments

.fusion-fullwidth-1 {
padding-left: px !important;
padding-right: px !important;
}

See what’s happened this past week in the world of forestry!

Does wildfire create home sweet home for bees? – Crosscut

Previously, little to no data existed on the effects wildfire and forest management practices have on native bee species, but thanks to scientists and technicians at Oregon State University, that’s starting to change.

How to protect your yard in freezing temperatures – The Florida Times-Union

The majority of the country is currently battling freezing temperatures, and southern states are seeing record lows. While a hard freeze can kill weeds and reduce pest problems, colder weather than normal puts plants at risk. Read these tips to find out how to take care of your plants before and after a freeze.

Eight New Year’s resolutions for a greener 2018 – GreenUP

Save money, feel healthier and be happier – all while helping the environment! These resolutions are the perfect way to boost your green power this year. Bonus: you’ll save money and feel healthier, too.

One million more dead trees in Calaveras – Recordnet.com

In California, bark beetle devastation continues even after droughts, bringing the total number of trees lost in Calaveras County since 2014 to about 3.3 million.

Good news for spotted owls – and thinning projects – Payson Roundup

Mexican spotted owls love the thickets of trees on the watershed of a reservoir in Payson, AZ. However, their dependence on the dense forests has delayed thinning projects necessary to prevent megafires in the area. A new study found that the owls do just as fine in thinner forests, as long as they still have groups of tall trees, making them (and the project) more adaptable.

Green space map to help preserve Olentangy River watershed – The Columbus Dispatch

As development pressure increases in Columbus, OH, the Friends of the Lower Olentangy Watershed group want to make sure natural space around the river is protected.

The post Forest Digest: January 7, 2018 appeared first on American Forests.

Sacred Roots: Trees in Folklore

January 3rd, 2018|0 Comments

.fusion-fullwidth-1 {
padding-left: px !important;
padding-right: px !important;
}

By Dylan Stuntz, American Forests

Humanity has understood the importance of trees for millennia — just look at the oldest forms of stories we have: folklore and myths. Trees have held sacred and important roles in many ancient theistic tales, and here are just a few culturally sacred trees in mythologies from around the world.

Acacia Tree (Egyptian Mythology)

The ancient Egyptians believed that the first gods were born under a sacred acacia tree, while other members of their pantheon emerged fully formed from the trunk. It was believed that life and death were decided by the gods under an acacia tree. The boat the sun god navigated the world on was made from palm fronds and acacias.

Yggdrasil the World Tree (Norse Mythology)

For the Vikings, this tree was so central to their mythology that they believed it held up the entire world! According to the Old Norse view of the cosmos, Yggdrasil was an immense ash tree that supported the nine realms, or the entire known universe. The gods lived at a realm at the center of the ash, with the branches stretching up supporting all nine of the existing worlds, including humanity.

The Sky-High Tree (Hungarian folklore)

Depiction of dragons at the top of the égig érő fa, found on Jacob’s Arch in Austria.

The égig érő fa is a tree from Hungarian folklore, and is featured in the story of a shepherd boy who ran into a tree that appeared to be without a top. He climbed and climbed, but the tree seemed to be endless. Once he reached above the clouds, he found himself in a magical realm full of fantastic creatures. It was believed that this endless tree reached all the way up into the heavens, while its roots intertwined with the deepest pits of the underworld.

Garden of the Hesperides (Greek Mythology)

In Greek mythology, a sacred apple grove found at the westernmost edge of the world was tended by nymphs, known as the Garden of the Hesperides. One bite of a golden apple found growing in the grove was said to grand immortality to anyone who dared to tread on this ground. Immortality did not come without a price, for guarding the grove was a hundred-headed dragon who never slept. According to myth, one of the apples from the grove was the source of the infamous Trojan War. The famous hero Hercules was commanded to steal an apple from the grove for one of his Labors.

The post Sacred Roots: Trees in Folklore appeared first on American Forests.